【导读】AI辅助人类,完成了首个非平凡研究数学证明,破解了50年未解的数学难题!在南大校友的研究中,这个难题中q=3的情况,由o3-mini-high给出了精确解。
就在最近,AI完成了首个非平凡研究数学证明!
完成这项研究的,是美国纽约布鲁克海文国家实验室凝聚态物理与材料科学分部的一位华人学者Weiguo Yin。

论文地址:https://arxiv.org/abs/2503.23758
在这项研究中,作者在一维J_1-J_2 q态Potts模型,通过引入最大对称子空间(MSS)方法,对其精确求解。
具体来说,作者将q^2×q^2的传递矩阵进行块对角化。
而q=3的情况,正是基于OpenAI的最新推理模型o3-mini-high来精确求解的。
在AI的帮助下,研究者成功证明,模型可以映射为一维q态Potts模型,其中J_2作为最近邻相互作用,J_1则作为有效的磁场,这一结果扩展了之前在q=2,即Ising模型的证明。
注意,这个问题,在数学界有50年没有解决。
论文引用了关于J_1−J_2伊辛模型(即q=2的Potts模型)的工作,这些工作可以追溯到1969年和1970年。
而o3-mini-high帮忙完成的这项证明,为众多悬而未决的物理问题(层状材料中原子或电子顺序堆叠的问题,以及非常规超导体中常见的T_c-拱形相的形成等),提供了全新的见解。
AI模型在科学研究中的巨大潜力,也再一次被证实!

Weiguo于2004年加入布鲁克海文国家实验室担任研究员,并于2006年晋升为助理物理学家,2008年晋升为副物理学家,2011年晋升为物理学家。
他的专长在于结合第一性原理、有效哈密顿量和机器学习方法,研究强关联体系、挫败磁性、超导性、多铁性、混合的3d-5d化合物、拓扑材料和非平衡态。
1998年,他获得南京大学的博士学位,并荣获2000年国家优秀博士学位论文奖。

五十年未解的数学难题,被AI解决了
在凝聚态物理、材料科学、量子信息学和微电子学等研究领域中,发现新的相和相变是一个核心挑战。
挫败磁体中存在许多不寻常的相,这些磁体通常用伊辛模型(Ising model)或量子海森堡模型(quantum Heisenberg model)来描述。
统计力学的第三个基本模型是q状态Potts模型。
它是伊辛模型(q=2)的推广,可以作为研究从离散(伊辛)对称性到连续(海森堡)对称性转变的有效中介。
特别是,一维J_1-J_2 Potts模型可能与众多问题相关,这些问题涵盖了从层状材料中原子或电子有序的面外堆叠,如1T-TaS_2 中的「大卫之星」电荷密度波,到每个时间步都有多种选择的时间序列问题,如乒乓球训练设计。
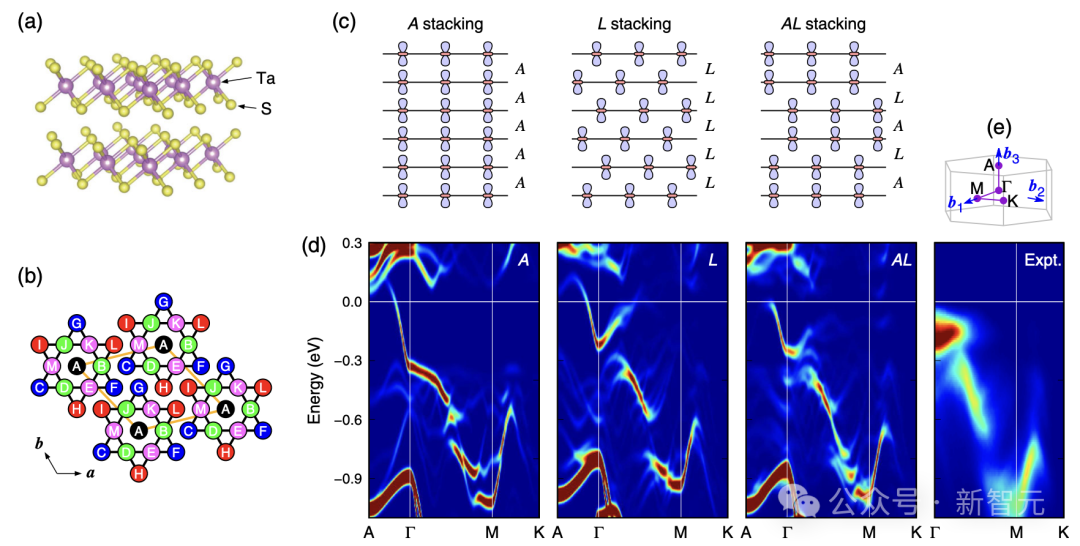
1T-TaS2中的「大卫之星」电荷密度波相关论文插图

一维J_1-J_2 Potts模型
尽管一维和二维的J_1-J_2伊辛模型和海森堡模型已被广泛研究,但只有一维J_1-J_2伊辛模型通过转移矩阵法得到了精确解。
对于一维J_1-J_2 Potts模型,至今仍没有精确的解析解。
因为当q=3时,该模型已经展现出与q=2(即伊辛模型)不同的基态相行为(见下图),因此精确求解任意q的模型具有基础性的重要性。
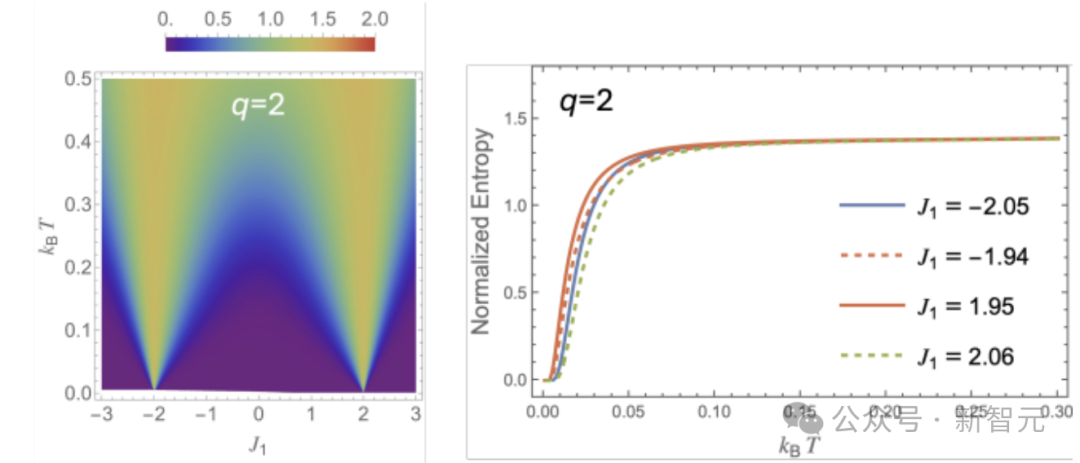
伊辛模型:不同的基态相行为
挑战在于转移矩阵的阶数迅速增加,阶数为q^2。
可想而知,q=3时的9×9矩阵已经很难进行解析求解,而q=10^10时的10^10×10^10矩阵,即使是数值计算也无能为力。
先前的研究将任务转化为数值计算有效的q×q矩阵,采用整数q形式的转移矩阵法,或连续q形式的转移矩阵。
尽管物理学的透明度较低,但仍然无法得到精确的解析结果。
因此,对于一维J_1-J_2 Potts模型,至今仍然缺乏其中丰富相行为的直观理解。
OpenAI o3-mini的创举:非平凡证明
最近的两个发展为这一长期未解问题提供了新的视角。
第一个发展是通过基于对称性的块对角化,将装饰伊辛梯形的4×4转移矩阵简化为有效的2×2矩阵。
这些发现为一维挫败Potts模型找到精确解,可能成为这一重要新方向的里程碑。
第二个发展是OpenAI最新的推理模型o3-mini-high,推导出了一个优雅的方程,在外部磁场下,可以确定装饰伊辛模型中UNPC的临界温度。
论文链接:https://arxiv.org/abs/2502.11270
因此,作者受到启发,逐步提示AI推理模型,去处理整数q形式的转移矩阵。
尽管AI的回答中有不少错误,针对q=3的情况,最终找到了一种基于对称性的块对角化方法,可以将一维J_1-J_2三状态Potts模型的9×9转移矩阵解析地简化为有效的2×2矩阵。
对于一般的q,关键的对称性是q个Potts状态的全排列对称性。
换句话说,哈密顿量(因此在整数q形式中的转移矩阵)在任何对标签{1,2,3,...,q}的排列下都是不变的;它的对称群是Sq。
虽然AI未能进一步推进,但警告说随着q的增大,排列的数量急剧增加。
然而,q=2和q=3的精确结果,特别是两者都归结为2×2矩阵,启发了作者:
由于在热力学极限下只有转移矩阵的最大特征值(λ)才重要,因此任务简化为识别包含λ的对称分离子空间。
随后,作者发现这个子空间由两个最大对称向量张成,因为所有转移矩阵元素都是正的,这使得最终得到了一个解析的2×2矩阵。
因此,任意q的一维J_1-J_2 Potts模型的精确解,就这样被找到了,而且过程出奇的简单!

o3-mini-high具体起了什么作用
下面我们就来看看,o3-mini-high是如何在这项研究



